FAµST is now compatible with CUDA 11 in addition to CUDA 9.2 which was already supported. The multi-version support is enabled on pyfaust and the same feature will be available soon on matfaust.
Author: Hakim
FAµST 3.7.2 / pyfaust support of float scalar type for both CPU and GPU implementations
Since FAµST 3.7.2 the float scalar type is managed by the available CPU and GPU implementations of FAµST algorithms (it concerns all the functions in pyfaust.fact, pyfaust.proj, pyfaust.poly).
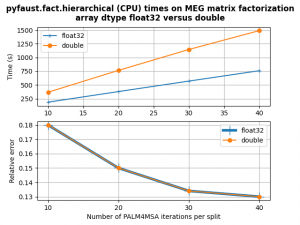
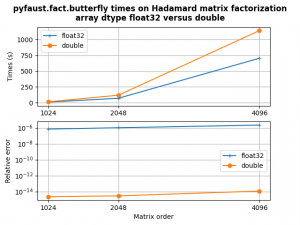
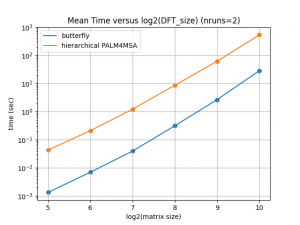
Obviously this new feature allows to optimize globally the running time of FAµST algorithms as the figures show below for the MEG factorization (pyfaust.fact.hierarchical) and the Hadamard factorization (pyfaust.fact.butterfly).
FAµST 3.6.3 / Faust optimizations Jupyter notebook and Matlab live script + Enhancement of FaustMulMode.DYNPROG algorithm
A new notebook about Faust optimizations is available for pyfaust and an equivalent Matlab live script is provided for matfaust.
These tutorials are an introduction to the Faust.optimize_time (matfaust, pyfaust), Faust.optimize_memory (matfaust, pyfaust) and Faust.pruneout (matfaust, pyfaust) functions.
This version optimizes also the FaustMulMode.DYNPROG method by taking the sparse matrices into account when calculating the complexity of matrix multiplications (hence the GREEDY method was abandonned).
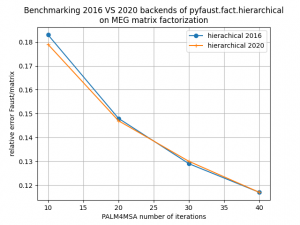
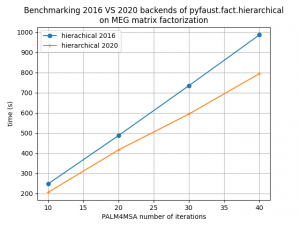
FAµST 3.6.0 / PALM4MSA and hierarchical algorithm 2020 implementations
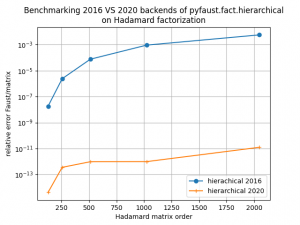
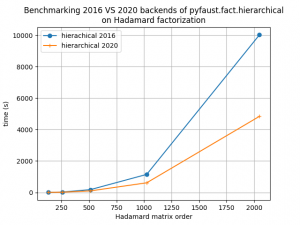
This version of FAµST accelerates the 2020 implementation of the PALM4MSA hierarchical algorithm. The figures below show how this implementation performs faster (and yet accurately) than the 2016 implementation of this algorithm on the Hadamard matrix factorization for different dimensions and also on the MEG matrix factorization.
FAµST 3.5.2 / Faust.optimize_time function
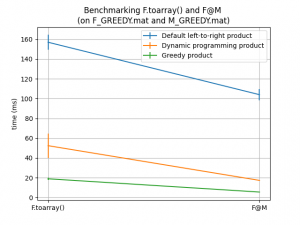
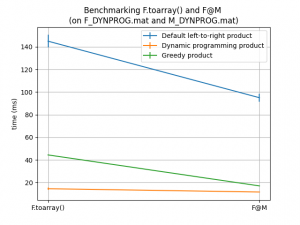
This version provides the stable function Faust.optimize_time() to optimize the calculation of Faust products (Faust full array or Faust-matrix product).
This function allows big speedups on certain Fausts as shown in the two examples below (where the speedups reach one order of magnitude).
Note: for a matter of reproducibility the .mat files F_GREEDY.mat, M_GREEDY.mat, F_DYNPROG.mat and M_DYNPROG.mat are provided in the faust data archive delivered by the matfaust or pyfaust packages (with auto-downloading if needed).
For further information about Faust.optimize_time you can look at the documentation for pyfaust or matfaust.
NOTE: the GREEDY optimization method was abandonned since FAµST 3.6.1 (cf. FAµST 3.6.3 news).
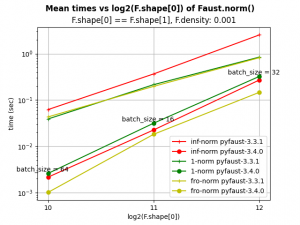
FAµST 3.4.0 / Faust.norm optimization
FAµST 3.3.0 / pyfaust/matfaust.Faust.butterfly algorithm
This version provides two ways to factorize a DFT matrix:
1. Calling matfaust/pyfaust.fact.hierarchical(DFT, ‘dft’) which uses behind the scene the new ParamsHierarchicalDFT simplified parameter structure.
2. Or calling matfaust/pyfaust.fact.butterfly(DFT) which is a new way to factorize hierarchically the DFT… and is faster than the hierarchical algorithm! More details will come later…
FAµST 3.2.8 / FAµST System packages/installers
System packages for MacOS X, Linux and Windows 10 are now publicly available.
They allow to install the Python and Matlab wrappers (pyfaust & matfaust) on these systems.
Note that for pyfaust the advised way to install is still to use the packages hosted on PyPI (through pip).
FAµST 3.2.1 / MHTP algorithms
This version of FAµST integrates a new algorithm that works hand in hand with the PAL4MSA algorithm.
This is the Multilinear Hard Thresholding Pursuit algorithm (MHTP) wich is a generalization of the Bilinear HTP algorithm discussed in [1].
This algorithm is available both for the pyfaust and matfaust wrappers but please note that it is still in experimental/beta status.
Related tutorials are available in the dedicated section of the website.
[1] Quoc-Tung Le, Rémi Gribonval. Structured Support Exploration For Multilayer Sparse Matrix Factorization. ICASSP 2021 – IEEE International Conference on Acoustics, Speech and Signal Processing, Jun 2021, Toronto, Ontario, Canada. pp.1-5. hal-03132013.
FAµST 3.1.0 / Exponential action of a matrix and FAµST poly module
A module named poly has been developed for matfaust and pyfaust (it is still in beta status though).
It allows among other functionalities to compute the action of the exponential of a matrix on a vector (using Chebyshev polynomial series).
This module is also GPU compatible.
A Jupyter Notebook is available to introduce how to use this module.
Reference: Sibylle Marcotte, Amélie Barbe, Rémi Gribonval, Titouan Vayer, Marc Sebban, et al.. Fast Multiscale Diffusion on Graphs. 2021. hal-03212764
Besides to this new module, a few optimizations of the Faust-matrix multiplications have been integrated (see the figures for the CPU, GPU implementations).