What’s new in this version of FAµST:
- First, new kind of projectors for PALM4MSA: spsymm, sptriu, sptril (more information on a specific use case is coming soon).
- Second, new options regarding the stopping criteria in PALM4MSA and the hierarchical algorithm. It is now possible to stop PALM4MSA if the error doesn’t change more than an arbitrary espilon (see the erreps parameter). It is also possible to interrupt the algorithm manually through the CTRL-C key combination at any iteration. This way you can stop the algorithm when the error satisfies your goal and in the same time you don’t have to wait any longer if the number of iterations set beforehand was too large.
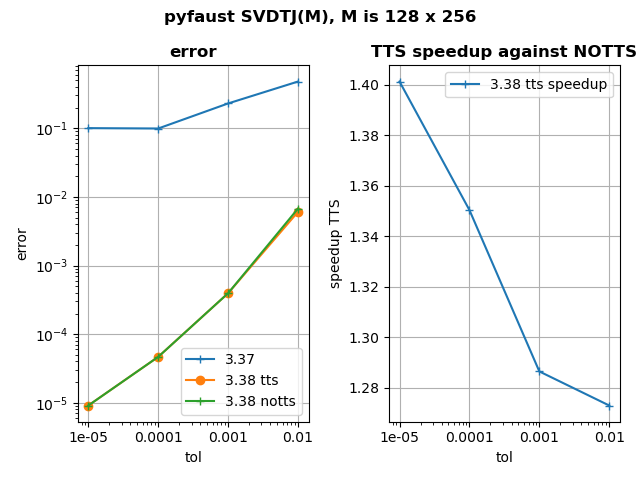
- Finally, SVDTJ has been thoroughly revamped. This algorithm computes a Faust approximation to the SVD factors of a matrix, using the truncated Jacobi method. Previously, the achieved accuracy could sometimes be worse than the targeted accuracy. This is now fixed. Besides, the computation of the error has been optimized to be faster. For more details, see the figure below in this news.
- In association to this new SVDTJ a function PINVTJ is now also provided in the FAµST API to compute a pseudoinverse approximate.
All these news apply both to pyfaust and matfaust.
Another noteworthy info is that the lazylinop module was splitted in another independent project that you can download from pip or anaconda.
The Matlab code will be published in a second time as soon as possible.
tol: the tolerance on relative error, which is e = || M – U S V’ ||_F / || M ||_F with M the matrix to factor
tts: two-times strategy in error computation, first the error computed is e’ = || M ||²_F – || S ||²_F because it is less costly. Then for the latest iterations e is computed because it is more accurate.
Here is a script to reproduce the data plotted in the figure.