We are glad to announce that the FAµST Inria Gitlab project is now public. We welcome all kinds of contribution: bug report, bug fix, new test, new feature and also documentation and tutorials. Here is our guide for contributing.
FAµST 3.39.2 — Sphinx API doc
A sphinx documentation is now available for pyfaust here.
FAµST 3.38.9 — CUDA support evolves
FAµST supports now CUDA 12 in addition to already supported CUDA 11. Note that CUDA 9 is no longer supported.
FAµST 3.38.0
What’s new in this version of FAµST:
- First, new kind of projectors for PALM4MSA: spsymm, sptriu, sptril (more information on a specific use case is coming soon).
- Second, new options regarding the stopping criteria in PALM4MSA and the hierarchical algorithm. It is now possible to stop PALM4MSA if the error doesn’t change more than an arbitrary espilon (see the erreps parameter). It is also possible to interrupt the algorithm manually through the CTRL-C key combination at any iteration. This way you can stop the algorithm when the error satisfies your goal and in the same time you don’t have to wait any longer if the number of iterations set beforehand was too large.
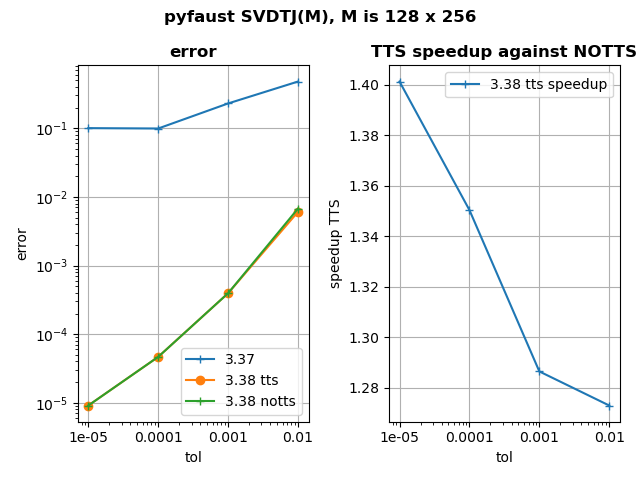
- Finally, SVDTJ has been thoroughly revamped. This algorithm computes a Faust approximation to the SVD factors of a matrix, using the truncated Jacobi method. Previously, the achieved accuracy could sometimes be worse than the targeted accuracy. This is now fixed. Besides, the computation of the error has been optimized to be faster. For more details, see the figure below in this news.
- In association to this new SVDTJ a function PINVTJ is now also provided in the FAµST API to compute a pseudoinverse approximate.
All these news apply both to pyfaust and matfaust.
Another noteworthy info is that the lazylinop module was splitted in another independent project that you can download from pip or anaconda.
The Matlab code will be published in a second time as soon as possible.
tol: the tolerance on relative error, which is e = || M – U S V’ ||_F / || M ||_F with M the matrix to factor
tts: two-times strategy in error computation, first the error computed is e’ = || M ||²_F – || S ||²_F because it is less costly. Then for the latest iterations e is computed because it is more accurate.
Here is a script to reproduce the data plotted in the figure.
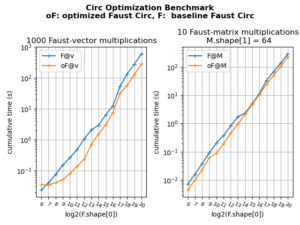
FAµST 3.36.0 — Optimization of circ, anticirc and toeplitz
This update of pyfaust provides an optimization of the pyfaust.circ function and also the anticirc and toeplitz functions which depends on the first one. The optimization is triggered using the diag_opt optional argument of those functions.
It is very similar to the pyfaust.dft optimization which relies on the butterfly structure of the Faust factors.
The figure below shows the result of a benchmark ran on circ with or without optimization:
The benchmark and plot scripts are available here: benchmark script, plot script.
NOTE: the same optimization has been implemented for matfaust too.
Edit 01/20 2023 — FAµST 3.37.0: the same optimization has been implemented on GPU too. It is available through the dev=’gpu’ and diag_opt=True arguments of the three functions).
FAµST 3.35.15 — LazyLinearOp
Edit — 17/08/2023: The LazyLinearOp class has been relocated in its own project named lazylinop
A new class named LazyLinearOp is now available in matfaust and pyfaust.
Starting from a numpy array, a scipy matrix, a Faust object, or potentially many other compatible linear operators with efficient implementatons, this class follows the lazy evaluation paradigm. In short, one can aggregate low-level LazyLinearOp objects into higher-level ones using many classical operations (addition, concatenation, adjoint, real part, etc.), without actually building arrays. The actual effect of these operations is delayed until the resulting linear operator is actually applied to a vector (or to a collection of vectors, seen as a matrix).
The main interest of this paradigm is to enable the construction of processing pipelines that exploit as building blocks efficient implementations of “low-level” linear operators.
LazyLinearOperators are complementary to other “lazy” objects such as LazyTensors in Kheops, or the ones of lazyarray, and WeldNumpy libraries, which, to the best of our knowledge, primarily provide compact descriptions of arrays which entries can be evaluated efficiently on the fly.
For more information and a demo about the LazyLinearOp class, a jupyter notebook is available here.
FAµST 3.33.5 — DFT / Butterfly Faust optimization
We optimized the DFT Faust product (pyfaust.dft / matfaust.dft).
The principle of this optimization is to simplify the butterfly matrix product to sums of diagonal matrix multiplications (likewise for the bit-reversal permutation).
This optimization is disabled by default, you need to use the diag_opt argument in order to use it.
In the figure below we show how it speeds up the Faust-vector and Faust-matrix products.
To reproduce the figure you can use these scripts: benchmark script, plot script.
We made this optimization available to any Faust composed of butterfly factors (Use the opt_butterfly_faust function in pyfaust or matfaust).
Special thanks to Simon Delamare and Rémi Gribonval who are at the source of this optimization.
FAµST 3.32.4 — DYNPROG product method GPU support
This version spreads the DYNPROG product method to GPU Fausts. This is a dynamic programming method to compute a Faust product (or a Faust-matrix product). It varies the order of matrix products composing the whole Faust product (aka Faust.toarray) considering the cost of each product to speed up the whole computation. Find more information about this method here.
The table below compares the computation times obtained using DYNPROG or DEFAULT_L2R methods (in the latter, the product is basically computed from the left to the right). Four Fausts are tested, they are dense, sparse (CSR, BSR matrices) or mixed (dense + sparse matrices).
The data for the table below was made using this script (please note that the script is random, so the results won’t be exactly the same from one run to another).
| Faust name | Product Method | Device | Faust matrix type | Comp. time (100 products) | Speedup vs DEFAULT_L2R | Number of factors |
|---|---|---|---|---|---|---|
| F1 | DEFAULT_L2R | GPU GTX980 | dense | 15.7 | 1 | 32 |
| F1 | DYNPROG | GPU GTX980 | dense | 4.8 | 3.3 | 32 |
| F2 | DEFAULT_L2R | GPU GTX980 | sparse (CSR) | 43.4 | 1 | 32 |
| F2 | DYNPROG | GPU GTX980 | sparse (CSR) | 17.7 | 2.45 | 32 |
| F3 | DEFAULT_L2R | GPU GTX980 | sparse (BSR) | 2.64 | 1 | 5 |
| F3 | DYNPROG | GPU GTX980 | sparse (BSR) | 1.75 | 1.5 | 5 |
| F4 | DEFAULT_L2R | GPU GTX980 | mixed (BSR + dense) | 6.26 | 1 | 14 |
| F4 | DYNPROG | GPU GTX980 | mixed (BSR + dense) | 2.77 | 2.26 | 14 |
FAµST 3.31.5 — Butterfly factorization with permutations
The butterfly factorization function has been updated to allow using one or several permutations. This update makes the function fully match the reference paper [1] and is available for both pyfaust and matfaust.
In addition to the permutation functionality of the butterfly factorization, a new function named rand_butterfly has also been integrated in the wrappers (pyfaust, matfaust). This function allows to randomly generate a Faust according to butterfly supports. It brings a simple way to test the butterfly factorization using the full array of those random butterfly Fausts.
[1] Quoc-Tung Le, Léon Zheng, Elisa Riccietti, Rémi Gribonval. Fast learning of fast transforms, with guarantees. ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, May 2022, Singapore, Singapore. (hal-03438881)
FAµST 3.30.0 — GPU Faust indexing optimization
The FAµST version 3.30.0 follows the previous news which showed the GPU Faust slicing optimization. This time this is the GPU Faust indexing that has been optimized. The figure below demonstrates how the optimization speeds up the related operations since the previous release (3.29.1).
 The code to reproduce the figure is available here.
The code to reproduce the figure is available here.
The figure was produced using a NVIDIA GPU GTX 980 configured with CUDA 11.