The Faust slicing on GPU has been optimized. The following benchmark compares some computation times of Faut slicings using pyfaust-3.27 and pyfaust-3.29 on GPU.

The method to optimize the slicing is similar to the one implemented on CPU before (see the related news).

The GPU used to produce this figure was a NVIDIA GTX 980. The scripts to reproduce are available here.

pyfaust and matfaust have been completed with Faust constructors to implement Direct Cosine Transform (DCT) and Direct Sine Transform (DST) of type II. In the figure below you’ll get an insight of the computation speed up brought by these new functions compared to their counterpart dense matrices. The benchmark is made on the multiplication by a vector (to apply the transform on a discrete signal).

The figure was produced on a 1.6 Ghz 4-cores CPU.

To reproduct the figure please use the scripts hosted on gitlab.

In this version you’ll find new Faust “constructors” in matfaust and pyfaust: toeplitz, circ, anticirc. As sparse Fausts these widely used functions in signal processing can spare memory and speed up many use cases.

In the figure below we show the acceleration allowed by the Faust versions of the functions compared to the corresponding full dense matrices built using scipy. The operations evaluated are the Faust-vector and matrix-vector products.

 The figure was produced on a 1.6 Ghz 4-cores CPU.

To reproduct the figure please use the scripts hosted on gitlab.

Anaconda packages are now available for pyfaust on Linux, Mac OS X and Windows.
Take a look at the documentation in order to install one of these packages in an Anaconda virtual environment.

This version of FAµST is a revamp of the Faust slicing and indexing implementations using a mechanism we call lazy slicing/indexing. It allows mainly to delay the Faust slicing and indexing operations by setting them virtually in order to avoid touching the Faust data until it is really necessary. Besides, some product related operations (as F[:, :N]@v) have been optimized based on this mechanism.

The figures below show the performance enhancement of these operations since the previous release of FAµST and make also a comparison to scipy which is outperformed on many cases. Scipy is used to implement an alternative Faust very basically as a Python list of scipy csr_matrix, for more details please look at the benchmark script.
The code to reproduce these figures is available on gitlab.
The figures were produced on a 1.6 Ghz 4-cores CPU.

BSR matrices are now supported on (NVIDIA) GPUs in matfaust and pyfaust.
The figure below shows how it can be faster to run BSR Faust products on GPU instead of CPU.

The script to reproduce these results is available here.

In this version, it is possible to factorize a matrix using PALM4MSA without any constraint on one or several factors. This is made possible by
the identity projector proj_id. In PALM4MSA when proj_id is used on a factor, the only change on the latter is made by the gradient descent (no other structure is imposed because proj_id simply does not modify the factor).
In particular, this is possible to factorize a matrix with the pyfaust.fact.hierarchical with no constraint at all on residual factors (except the last one which composes the output Faust and so needs to be constrained). Several tests have been made and we’ve seen that the Hadamard matrix factorization works pretty well without residual constraints on the condition that the skperm projector is used (rather than the less accurate splincol projector which gave bad results). We’ve seen also that it is possible to factorize the MEG matrix (hierarchical, section 6.) with, here again, no constraints on residual factors without observing a drop in accuracy.
The best advantage of these light configurations, is to naturally define the constraints of the targeted Faust we need to obtain through the factorization without making assumptions on the residual factors structures. Only the factors that actually compose the Faust are constrained.
Although, this new feature needs further considerations, it is made available to make possible for anyone to pursue some experiments.

For more details and in order to test if by yourself, please look at: pyfaust.fact.hierarchical (5. and 6.), pyfaust.fact.ParamsHierarchicalNoResCons, pyfaust.fact.ParamsHierarchicalWHTNoResCons, pyfaust.fact.ParamsHierarchicalRectMatNoResCons.

Other enhancements in this version:
– Smoother non-consistent constraints error handling in pyfaust.fact.palm4msa and pyfaust.fact.hierarchical (avoiding a python runtime crash and giving more informative error messages). This enhancement is yet to add to matfaust.

– Several recent bugs have been corrected (in particular, bugs dating from FAµST 3.20 which switched to matlab interleaved complex API).

This versions of FAµST brings several enhancements and complements to BSR matrices API, power iteration/2-norm algorithms and matfaust.Faust in single/float precision.

– Integration of BSR matrices in DYNPROG algorithm (beta).
– More information displayed on BSR matrices when a Faust is printed out.
– Faust.factors is able to return a BSR matrix too with pyfaust and a CSR sparse matrix copy with matfaust (Matlab doesn’t support BSR matrices).
– matfaust/pyfaust.rand_bsr is capable to generate complex random BSR Fausts with nonzero imaginary part.
– Random vector initialization in power iteration algorithm, and workaround of the float accuracy issues when used on a Faust.
– Also securing the spectral norm/2-norm computation of a Faust (a null Faust has zero norm, no need to go further in calculations).
– matfaust.Faust.single allows to convert a double Faust to a single/float Faust (see also this FAQ entry).

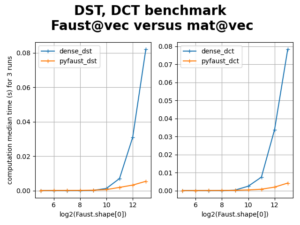
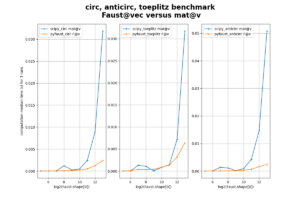
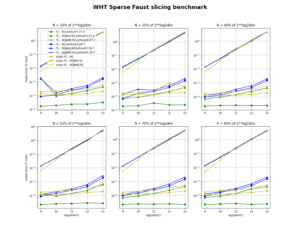
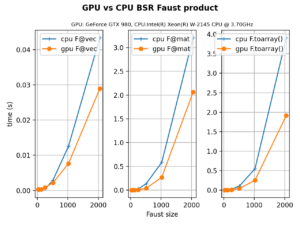
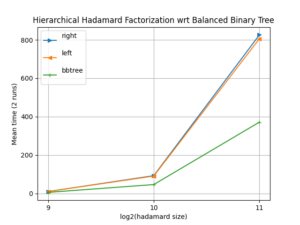
FAµST 3.25.3 version is an optimization update of the balanced tree
butterfly factorization C++ implementation (API links: matfaust, pyfaust).

As the following figure shows, the FAµST implementation is faster than the paper reference [1] python scripts [2] by about an order of magnitude for large dimensions of the Hadamard matrix.
The gap is due to the code parallelization (which is possible because of the bbtree structure of the factorization) and use of CSR sparse matrices for the supports and factors (instead of dense matrices).

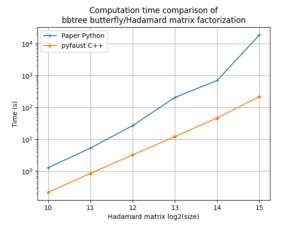
Note: the computer used to produce the figure data provides 1450Gio of RAM, and 64 cores (Intel(R) Xeon(R) Gold 5218 CPU @ 2.30GHz).

Brief examples of how to use the pyfaust/matfaust butterfly functions are available on these pages: matfaust, pyfaust.

[1] Quoc-Tung Le, Léon Zheng, Elisa Riccietti, Rémi Gribonval. Fast learning of fast transforms, with guarantees. ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, May 2022, Singapore, Singapore. ⟨hal-03438881⟩

[2] Léon Zheng, Quoc-Tung Le, Elisa Riccietti, Rémi Gribonval. Code for reproducible research – Fast learning of fast transforms, with guarantees. 2022, ⟨swh:1:dir:42d42bf905c9f3bbcd6cf5e1e0cda6be2d0d63de;origin=https://hal.archives-ouvertes.fr/hal-03552956;visit=swh:1:snp:6a2256426a0f3a7491086fbf2da554d7589d1e18;anchor=swh:1:rel:f477382c82ada89647864605ea44b12383c04167;path=/⟩. ⟨hal-03552956⟩

This version of FAµST adds the binary balanced tree implementation of the butterfly hierarchical factorization. As you can see in the following figure it speeds up the factorization about a factor of two compared to right/left hierarchical factorization.

Reference: Léon Zheng, Elisa Riccietti, Rémi Gribonval. Hierarchical Identifiability in Multilayer Sparse Matrix Factorization. 2021. ⟨hal-03362626v2⟩